



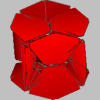


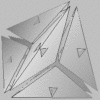


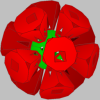

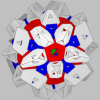

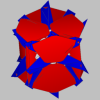



This holyhedron consists of nine layers. Each image in the first row shows a single one of these layers, while the corresponding image in the second row shows all layers up to and including that one. The final image in the lower right corner is the full holyhedron. Click on any of the small images to view a larger version of it.
| 12 faces | 12*6 = 72 faces | 20*4 = 80 faces | 30*4 = 120 faces | 12*6 = 72 faces | 20*4 = 80 faces | 4*4 = 16 faces | 6*4 = 24 faces | 4*4 = 16 faces | |
|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|

| |

|

|

|

|

|

|

|

|

|

The excellent program JavaView was used to model the holyhedron and to render these images.
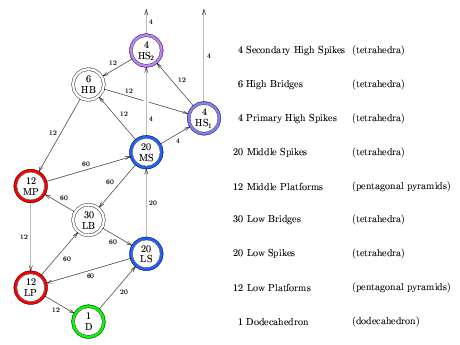
The following graph shows the "piercing relation" among the layers;
it is a schematic of which parts pierce which other parts of the holyhedron,
and may be helpful in understanding what is going on in the pictures
above.
The nine nodes in the graph represent the nine layers of the holyhedron,
colored the same as in the above images.
The label on each graph edge is the number of piercings
that the "from" layer makes into the "to" layer.
The two graph edges leading nowhere from the High Spikes nodes
represent the eight vertices on the convex hull of the holyhedron,
which don't pierce anything.
Postscript version (suitable for printing)
|
Last Modified: Fri May 23 23:15:29 PDT 2003 Don Hatch hatch@plunk.org |
|