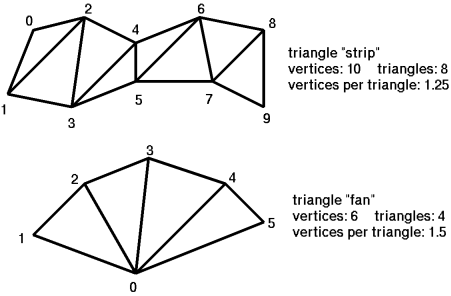
TC, or "triangle consolidator", constructs triangle strips or triangle fans from independent triangle data. The geometric transformation of 3D points onto a 2D screen involves some heavy math, and you can realize a performance benefit by reusing the results of that math where possible. Each new triangle strip or fan is constructed from one of the edges of the previous triangle and a new vertex.

You can achieve 3x performance minus the cost of transforming the first two vertices per strip. Thus it's important that strips and fans are made as long as possible (fewer strips and fans). Some architectures have a maximum preferred strip length, after which the engine may stall.
I wrote meshifier in 1995 because Sharon Clay at Silicon Graphics asked me how I might construct strips from a lattice of triangles as an interview question. It has some fundamental architectural limitations. Some, like an error in the reset code and being able to specify that triangles should not be output in reverse order, have been fixed by Neal Tringham and are incorporated in the new version available from his web page. Others, such as the limitation on numbers of vertices and connectivity, are harder to repair.
In "TC" I've attempted to fix those old errors. TC attempts to consolidate triangles limited only by the limits of the machine' available memory and speed. I have changed the API, using OpenGL as a loose model (although OpenGL arguably has its shape because it provides a hardware abstraction layer), so that more algorithmic abstractions and optimizations are possible. I have tried to build in features which are useful to modelers and offline optimization tools, such as whether or not to honor vertex ordering. I have also spent a few days trying to test the code nominally and attempt to have some confidence that even its low-memory behavior is predictable.
I hope you find it useful. ---Brad Grantham
The namespace of all functions and identifiers in TC is protected using
the initials of my software organization Applied Conjecture and
TC. All functions in TC are prefixed with actc.
All symbolic constants and #defines are prefixed with
ACTC_. All exported data structures are prefixed with
ACTC.
ACTCData consolidator object is created using the
following code. This structure contains state data about optional
parameters and triangle connectivity. actcNew returns
either an initialized ACTCData object if successful or
NULL if memory cannot be allocated.
#include <ac/tc.h>
ACTCData *tc;
tc = actcNew();
if(tc == NULL) {
/* memory allocation failed */
/* print error here and exit or whatever */
}
Any errors encountered during execution are typically both returned as
results from a TC function and stored in the structure. The error
can be retrieved using actcGetError. Here is an example of adding a
triangle and checking the error.
actcAddTriangle(tc, v1, v2, v3);
if((e = actcGetError(tc)) != ACTC_NO_ERROR) {
/* something bad happened */
/* print error and exit or whatever */
}
A more compact representation may not use actcGetError at
all, since many functions return either the error or
ACTC_NO_ERROR.
if((e = actcAddTriangle(tc, v1, v2, v3)) != ACTC_NO_ERROR) {
/* something bad happened */
/* print error and exit or whatever */
}
Since the error is reset in the structure by
actcGetError, it makes sense to go with either one style or
the other, to avoid being confused when a later return from
actcGetError returns an error which has already been
handled. Errors are represented by negative integers, so some
functions may return non-error information as a positive integer.
Slightly smarter applications may try
to detect some failure conditions and proceed after some kind of
repair.
actcAddTriangle(tc, v1, v2, v3);
e = actcGetError(tc);
if(e == ACTC_ALLOC_FAILED) {
/* couldn't alloc memory using one of the malloc(3) family */
/* application can free unused memory and try again */
} else if(e != ACTC_NO_ERROR) {
/* something bad happened other than malloc failure */
/* print error and exit or whatever */
}
For simplicity, examples in the remainder of the programmers' guide will not
check for errors but will mention where errors may occur. Several
functions can result in the error ACTC_DATABASE_CORRUPT but are not
noted here; that particular error return indicates corruption of
ACTC's internal data structures and really requires debugging (as
described below).
ACTC_OUT_HONOR_WINDING symbolic constant. These values are set
by actcParami and retrieved by actcGetParami.
int isHonoringWinding;
actcParami(tc, ACTC_OUT_HONOR_WINDING, ACTC_TRUE);
actcGetParami(tc, ACTC_OUT_HONOR_WINDING, &isHonoringWinding);
actcGetParami accepts two additional symbolic
constants which may
not be set by the application. ACTC_MAJOR_VERSION and
ACTC_MINOR_VERSION return the major version number and
minor version number, respectively.
Parameters are differentiated by the direction of the data they
control. OUT parameters control how TC hands its
consolidated primitives back to you. IN parameters tell
TC the limits you intend to guarantee on your input data, which may
used for optimization purposes. ALG parameters directly
affect the internal algorithms used by TC. Some parameters require
the extended range of unsigned int, and they can be set
and queried by actcParamu and actcGetParamu,
but both sets of Param... functions take the same symbolic
constants and convert to-and-from the range of their parameter or
return variable. Here are the parameters available in TC 1.1:
| Enumerant | Data type | Meaning | Prefer Paramu |
|---|---|---|---|
| ACTC_OUT_MIN_FAN_VERTS | integer | Minimum number of vertices returnable in a triangle fan | No |
| ACTC_OUT_HONOR_WINDING | boolean | Whether triangles may be output in reverse vertex order | No |
| ACTC_OUT_MAX_PRIM_VERTS | integer | Maximum number of vertices to output in a primitive | No |
| ACTC_IN_MIN_VERT | integer | Minimum vertex index | Yes |
| ACTC_IN_MAX_VERT | integer | Maximum vertex index | Yes |
| ACTC_IN_MAX_VERT_SHARING | integer | Maximum number of edges that will share a vertex | No |
| ACTC_IN_MAX_EDGE_SHARING | integer | Maximum number of triangles that will share an edge | No |
If called during INPUT or OUTPUT,
actcParami can result in ACTC_DURING_INPUT,
or ACTC_DURING_OUTPUT, respectively. If called to set
ACTC_IN_MIN_VERT or ACTC_IN_MAX_VERT so the
vertex range is negative, or to set
ACTC_OUT_MAX_PRIM_VERTS to less than 3, or to set a value
associated with a symbolic constant ACTC does not know about, then the
error ACTC_INVALID_VALUE will result.
actcParami(tc, ACTC_OUT_MAX_PRIM_VERTS, 14);
actcBeginInput(tc);
actcAddTriangle(tc, 1, 2, 3);
actcEndInput(tc);
actcBeginOutput(tc);
prim = actcStartNextPrim(tc, &v1, &v2);
actcGetNextVert(tc, &v3);
actcEndOutput(tc);
/* v1, v2, and v3 are now set to 1, 2, and 3. */
actcEndInput and actcEndOutput are intended as
checkpoints for optimization, compaction, etc. Your application can
call actcGetIsDuringInput and
actcGetIsDuringOutput to determine if the TC object is
currently ready in the input or output stages (or is otherwise idle).
If actcParami is called during input or output, an error of
either ACTC_DURING_INPUT or ACTC_DURING_OUTPUT
results, respectively.
actcAddTriangle, and the possible results may be
ACTC_DURING_OUTPUT if TC is in output mode,
ACTC_IDLE if TC is not in input mode, or
ACTC_ALLOC_FAILED if an internal data structure could not
be allocated. In the last case, the database is not altered. An
application could perform compaction on its own data and try
actcAddTriangle again, or it could attempt to retrieve all
the primitives currently available from the database. This would
probably give worse results (more primitives, fewer vertices per
primitive) than retrieving primitives from the complete database but
may be better than getting no primitives at all.
int triCount;
int tris[][3];
actcBeginInput(tc);
for(i = 0; i < triCount; i++)
actcAddTriangle(tc, tris[i][0], tris[i][1], tris[i][2]);
actcEndInput(tc);
unsigned int, and so
anywhere from 0 to UINT_MAX, inclusive. Internal data
structures allow quantity INT_MAX vertices, edges, triangles,
vertex valences, and edge valences to be input. With the data
structures TC uses
as of version 1.1, on most machines at the time of writing, a process'
memory space will be exhausted before the range of any of these items
is exhausted. As of version 1.1, TC has not been tested on an
architecture with integers or pointers larger that 32 bits.
actcStartNextPrim. The primitive type is returned, either
ACTC_PRIM_STRIP or ACTC_PRIM_FAN.
actcStartNextPrim may also return
ACTC_DATABASE_EMPTY if all triangles input so far have been
returned in primitives. actcStartNextPrim stores the first
two vertices by reference, and
actcGetNextVert provides each subsequent vertex.
actcGetNextVert will return ACTC_PRIM_COMPLETE
when their are no more vertices to return.
int prim;
int v1, v2;
actcBeginOutput(tc);
while((prim = actcStartNextPrim(tc, &v1, &v2) != ACTC_DATABASE_EMPTY) {
/* start a primitive of type "prim" with v1 and v2 */
while(actcGetNextVert(tc, &v3) != ACTC_PRIM_COMPLETE)
/* continue primitive using v3 */
}
actcEndOutput(tc);
actcTrianglesToPrimitives which inputs triangles and
extracts primitives, including attempting to recover from low-memory
situations by first draining the primitive database, and then by
cleaning up unused memory if draining is not sufficient. Since TC
cannot know in advance how many primitives it can find (and thus how
many vertices), the application will have to provide primitive storage
large enough to hold the input data as independent triangles. The
application may also tell actcTrianglesToPrimitives how
many triangles to input to TC before draining the database.
The following example shows how an application might call
actcTrianglesToPrimitives; here the application has provided
INT_MAX as the maximum batch size in triangles, which
effectively means input all the triangles first before outputting.
int triangleCount;
int triangles[][3];
int *primLengths;
int *primVerts;
int *primCount;
/* get triangleCount and triangles from somewhere */
primLengths = (int *)malloc(sizeof(int) * triangleCount);
primTypes = (int *)malloc(sizeof(int) * triangleCount);
primVerts = (int *)malloc(sizeof(int) * 3 * triangleCount);
primCount = actcTrianglesToPrimitives(tc, triangleCount, triangles,
primTypes, primLengths, primVerts, INT_MAX);
if(primCount < 0) {
/* something bad happened */
/* print error and exit or whatever */
}
actcTrianglesToPrimitives calls
actc{Begin,End}{Input,Output}, actcAddTriangle,
actcGetNext{Prim,Vertex}, and actcMakeEmpty.
It returns any unrecoverable error it may receive from these functions,
or it will return the total number of strips and fans it finds. The types
and length in vertices of all primitives are stored in primTypes and
primLengths, and then the vertices for each primitive in turn are
stored sequentially in primVerts.
actcGetMemoryAllocation to make TC search how much
memory is being used in data structures. This may be an expensive
operation in TC 1.1 in that it searches the allocated data structures.
actcDumpState to print out the internal state of a TC
object (in no particular format). In order for me to help you debug a
problem, it would be useful to print out the TC version number, the
triangles you input to TC (in the order you input them), and the
output of actcDumpState at the beginning and end of your
output phase. actcDumpState has no return value.
actcMakeEmpty; the TC object will
be reset to idle, contain no triangles, and will be ready for another
set of input triangles. actcMakeEmpty returns any error
that occurs during cleanup, but for the 1.1 release it can only return
ACTC_NO_ERROR.
To free the memory associated with a TC object, call
actcDelete with the pointer to the object; this function
effectively calls actcMakeEmpty and then frees the TC
internal data. Further use of that TC object pointer will have
undefined results but will probably crash your application.
ACTC_OUT_MIN_FAN_VERTS to INT_MAX. Technically, a very
large triangle fan could still be formed, but when someone creates a
two billion vertex triangle fan with TC, I will consider it a success
rather than a failure.
actcParami(tc, ACTC_OUT_MIN_FAN_VERTS, INT_MAX);
ACTC_OUT_MAX_PRIM_VERTS to set the maximum number of vertices to produce
per primitive.
actcParami(tc, ACTC_OUT_MAX_PRIM_VERTS, 12);
ACTC_OUT_HONOR_WINDING to FALSE or 0. This has the effect of allowing
a triangle to be included in a primitive even if its vertices would
be drawn in reverse order. Note that every odd triangle in a strip
(counting from 0) will normally be wound backwards if winding is
honored.
actcParami(tc, ACTC_OUT_HONOR_WINDING, ACTC_TRUE);
.a
library. The makefile provided by default has targets for the library and
the sample programs:
make libactc.a
To turn on some simple debugging assistance, compile TC with the
DEBUG preprocessor symbol defined (-DDEBUG
for most UNIX compilers). Error conditions should print the reason
and the function in which the error occurred. Any function finding an
unexpected inconsistency in data structures (like performing a table
search and not finding an element which must be there) will call
abort() and presumably dump core. I wouldn't expect any
ordinary application developer to be able to debug TC from a core
file, of course. If INFO is also defined, then the
abort() call will be preceded by a dump of the internal
data structures in tc. If you would like me to debug TC based on your
input, it would help me to have this output as well as the set of
triangles originally input to TC.
actctest program makes sure the basic TC functions
work. If it prints anything when compiled with actc.c without
DEBUG and INFO, then something bad
happened.
The actctest2 program repeatedly inputs random data into TC
and makes sure it gets the same thing out as it received. You can
specify settings for any of the OUT parameters, and change the
seed that actctest2 uses to initialize the random number
generator.
The actcsample program takes in a particular word-based format
containing
vertices and triangles, and converts that data into strips and fans. It
passes the vertex list through verbatim. Someone could
use this either as an element in a tool pipeline or as the basis for a
new offline or interactive stripping tool. Here's what the input format
looks like:
[x y z nx ny nz r g b]
[x y z nx ny nz r g b]
[...]
end
triangle v1 v2 v3 end
[triangle v1 v2 v3 end]
[...]
end
In this example, x, y, and z are the vertex coordinates,
nx, ny, and nz are the vertex normals, and
r, g, and b are the vertex colors. The set of
vertices are terminated by the word end. Vertices are
optional and are only passed straight through. For each triangle, v1,
v2, and v3 are the indices of each vertex in the triangle.
Each triangle is terminated by the word end, and the list
of triangles is terminated by end. The output format is
similar, except that the triangle section is replaced by a list
of primitives. Here's what the output format looks like:
[x y z nx ny nz r g b]
[x y z nx ny nz r g b]
[...]
end
strip v1 v2 v3 [v4 [v5 [...]]] end
fan v1 v2 v3 [v4 [v5 [...]]] end
[...]
end
Running
actctest2, and it will need tweaking on anything
but Linux, IRIX, and Windows 98. If you'd like to submit a patch to
"timer" for another operating system, I will place it on my web page
and incorporate it into TC.
I have tested TC's performance against an optimized meshifier modified by Randall Frank at Lawrence Livermore National Labs and meshifier appears to run about twice as fast, probably because it doesn't check for errors internally very well and makes some assumptions about vertex and edge connectivity. Perhaps TC could approach that performance level if the internal consistency checks were made to compile conditionally.
The algorithm attempts to remove all the triangle fans first. I've found
that this works for fewer than half of the simple data files I've tried.
For 1.1 the default value associated with ACTC_OUT_MIN_FAN_VERTS
is set to INT_MAX. Other good values appear to be near 8 and 16. You'll
have to try it yourself to see how it works with your data.
One could conceivably implement simulated annealing with TC. An application would repeatedly calculate solutions to triangle sets with TC, swapping the order of some number of triangles, each time choosing the better solution. As time goes on, the number of triangles rotated could be reduced. Simulated annealing will typically give a pretty good solution while allowing the application to choose how much time it cares to spend to find a solution.
Revision Control Information: $Header: /home/grantham/cvsroot/projects/web/actc/manual.html,v 1.5 2000/11/22 20:19:36 grantham Exp $