Geodesic Domes

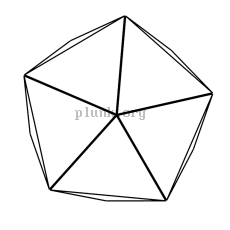
For Burning Man 2006, my old friend and new camp-mate Jack Smith invited me to help him on a project to add lights to some of the struts of one of our camp's domes. The lights would be controlled from a computer so that we could light up the dome in all kinds of fun patterns. As part of my contribution, I wrote a controller for the dome light sequences and then a dome simulator which showed a geodesic dome in three dimensions and displayed light sequences like the finished project would. I hope to talk in more detail about the lighting project in a later post.

In order to build the 3D simulation program for the dome, I had to figure out what the structure of our dome actually is. I'd like to share what I learned about geodesic domes.

Motivation

Everyone at Burning Man has a geodesic dome. Okay, not everyone has one, but it sure seems like that. (I have one of those dumb six-post Sears canopy thingies.) There are lots of domes of different sizes and degree. The geodesic dome structure is dictated by some geometry and some math. Here's an image I've rendered of a geodesic "5/8 3v" dome. (I'll explain what "5/8" and "3v" mean later.)

A "geodesic" dome

The invention of the geodesic dome is credited to Buckminster Fuller but is reported to have been invented 25 years earlier by Walter Bauerfeld for work on a planetarium projector at Carl Zeiss optics.

Geodesic Dome Geometry

Geodesic domes don't have one canonical form, but the most popular is based on an icosahedron whose triangular faces are then subdivided into smaller triangles. An icosahedron has twenty faces, each of which is an equilateral triangle and therefore all of the triangles are the same size. As you can see in the picture below, an icosahedron appears to have a cap and then a base made up of five triangles all sharing the top and bottom points, respectively. Ten triangles connect the cap and base. Wikipedia has a quite extensive and bewildering page about icosahedra.


An icosahedron viewed from the "top"		An icosahedron viewed from the "side"

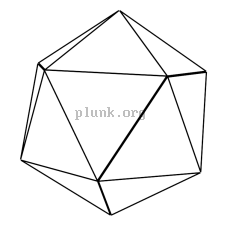
In case you want it, here's a text file of the corners, edges, and triangles that make up an icosahedron.

Triangles are structurally very strong. If you lean on one of the corners of a triangle made from three pipes bolted together, the only way it can collapse is if one of the pipes actually buckles or if a nut completely shears off of a bolt. It's much stronger than a rectangle; a rectangle of pipes and bolts could collapse if the bolts slip, which is much more likely than a shear. The canopy thingy I bought from Sears really can't stand up to the wind because it's all rectangles. (Cross-brace ropes helped somewhat in 2004 and 2005, but increased the stress on the struts.)

The force put into a corner of a triangle is directly transmitted to the base of the triangle. Since an icosahedron is made up of triangles, the force is distributed throughout the shape. The icosahedron can collapse from one of the joints between separate triangles bending, but that's still a very strong structure.

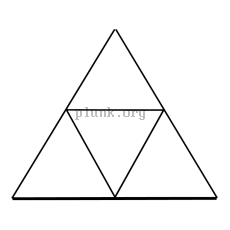
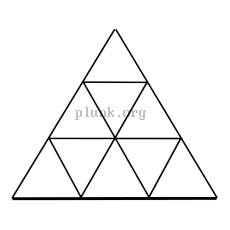
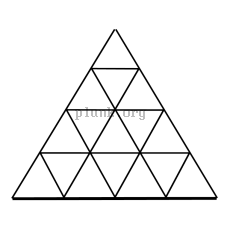
To make an icosahedron approximate a sphere more closely, the triangles making up the icosahedron are subdivided by splitting the edges of the triangle and then making the new split edges into more triangles. As in the pictures below, splitting each edge into n new edges yields n² new triangles.


A triangle whose edges are split into 2; the result is 4 triangles		A triangle whose edges are split into 3; the result is 9 triangles		A triangle whose edges are split into 4; the result is 16 triangles

The popular notation on the web for this seems to be mV, where m is the number of new edges made from each original edge, like 2v, 3v, 4v, etc...

If the corners of the new triangles are then moved out to the surface of a sphere centered on the icosahedron, you get something that looks more and more like a sphere the more the triangles are split. These are called "geodesic spheres". Here are geodesic spheres where the initial edges are split into 2 edges (resulting in 80 triangles), 3 edges (180 new triangles), and 4 edges (320 new triangles). I've thrown in one with 10 new edges from each initial edge, yielding 2000 triangles, 100 for each original triangle on the icosahedron.


A 2v geodesic sphere (80 triangles)		A 3v geodesic sphere (180 triangles)


A 4v geodesic sphere (320 triangles)		A 10v geodesic sphere (2000 triangles)

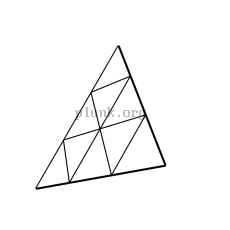
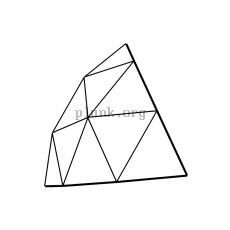
To make a geodesic dome, you cut a geodesic sphere in half.

Spheres with an odd degree (1v, 3v, 5v, etc...) can't actually be cut exactly in half. There's a ring of triangles that span the middle of the sphere, so typically you choose to split either just above or below that ring. For 3v domes, the popular name on the web for splitting above or below the ring seems to be "3/8" and "5/8", respectively. Here are pictures of 2v, 3/8 3v, 5/8 3v, 4v, and 10v geodesic domes.


A 2v geodesic dome		A "3/8" 3v geodesic dome		A "5/8" 3v geodesic dome


A 4v geodesic dome		A 10v geodesic dome

(I'm not really sure why the two variants of the 3v domes are called "3/8" and "5/8". There are 9 edges in a zig-zag from the top of a 3v sphere to the bottom, so it seems to me like "4/9" and "5/9" would be better names.)

Actually Building a Dome

One interesting thing about the process of splitting the triangles and then moving ("projecting") the corners out to the surface of a sphere is that the edges change so they are no longer equal lengths. Thus the triangles are no longer equilateral. The math is a little complicated to get right. (I wrote a program to do it.) I've provided a picture below of a single 3v triangle before and after projecting onto the sphere, including the new lengths if the original triangle was 3 meters on each side.


A 3v triangle before projection		A 3v triangle after projection		Lengths of edges of projected triangles

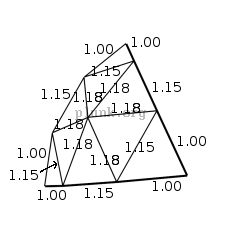
This is why sites like Desert Domes are so useful to dome builders; the Desert Domes site provides the ratios of strut lengths for domes of the most common degrees.

You can see that there are only three unique lengths; 1.00, 1.15, and 1.18 meters. One way to provide an easy template for building such a dome is to color code the struts, and provide a diagram of how the final dome looks with colored struts. For example, let's color the 1.18-meter struts green, the 1.15-meter struts orange, and the 1-meter struts blue.


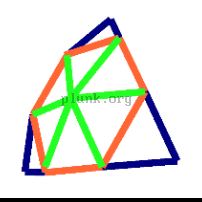A 3v triangle		Edges colored by length

As an aside, if you were to make a "5/8" 3v dome with struts of 1, 1.15, and 1.18 meters, the dome would be 5.7 meters across. (nearly 19 feet)

Our domes at Burning Man were 5/8 3v domes. I've prepared a text file with the geometry of a 5/8 3v dome , in case you want it. Here are a pair of images showing those kind of domes with color-keyed struts.


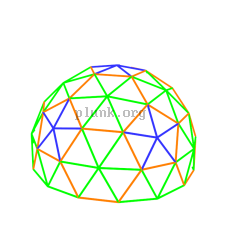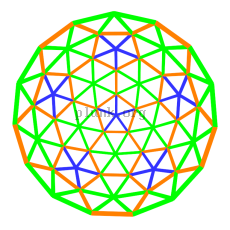View of 5/8 3vdome colored by strut length		Layout map of dome struts colored by length

One way to construct a dome is to cut lengths of pipe (steel pipe or electrical conduit if strength is less important), crimp the ends, drill holes through the ends, and then bolt all the pipes together at the dome corners. This seems to be very popular, probably because it's easy. The pipes can also be bolted to plates that form the corners of the dome, but this takes a little more work and is slightly less stable with only one hole in each end of each pipe.

Here's a picture of the Karma Chickens' dome at Burning Man 2006, made from bolted-together electrical conduit, with dome coverings on it and a little storage quonset attached to it. I don't take any credit for this dome; it and another just like it were designed long before I joined the Karma Chickens' camp. At least this year I did help raise the domes on the playa.

(We didn't finish the lighting project. Maybe next year I'll have pictures of that.)

Last modified:
Sun Oct 1 12:25:57 PDT 2006