







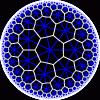

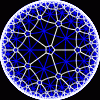
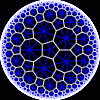



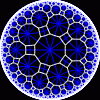
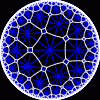


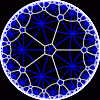
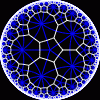
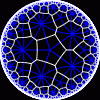

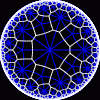
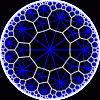
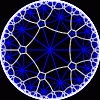

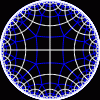
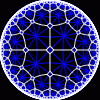






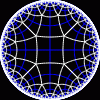
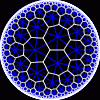





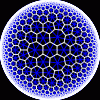


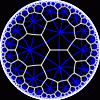



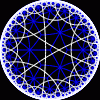

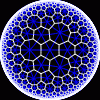

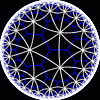
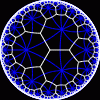
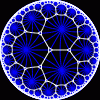
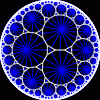
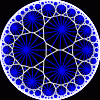
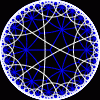
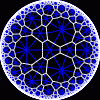
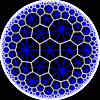
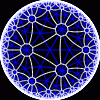
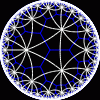
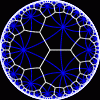
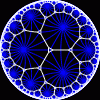
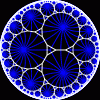
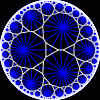
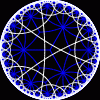
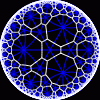
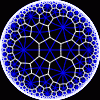
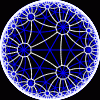
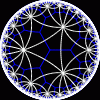
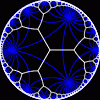
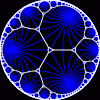
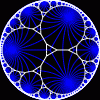
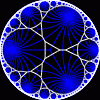
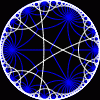
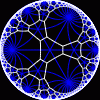
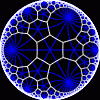
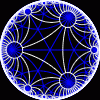
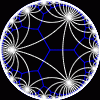
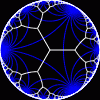
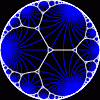
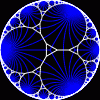

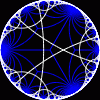
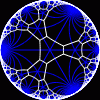
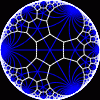
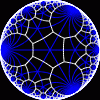
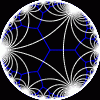
another
view





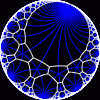
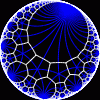


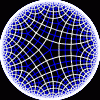
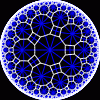
Each tesselation is represented by a Schlafli symbol of the form {p,q}, which means that q regular p-gons surround each vertex. There exists a hyperbolic tesselation {p,q} for every p,q such that (p-2)*(q-2) > 4.
Each tesselation is shown in various stages of truncation.
The dual of each tesselation or truncated tesselation is shown in blue. At the final stage of truncation (4.0) the object becomes its dual so those images are identical to the untruncated images except that the colors are reversed.
You may want to make your browser window wide so you can see them all at once. Click on an image to see a bigger version of it.
| Truncation: | 0 | .5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 (dual) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| {3,7} |

|

|

|

|

|

|

|

|

{4,5}
|
| 
| 
| 
| 
| 
| 
| 
| 
| 
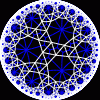
{5,5}
|
| 
| 
| 
| 
| 
| 
| 
| 
| 
{5,4}
|
| 
| 
| 
| 
| 
| 
| 
| 
| 
{7,3}
|
| 
| 
| 
| 
| 
| 
| 
| 
| 
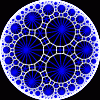
{8,3}
|
| 
| 
| 
| 
| 
| 
| 
| 
| 
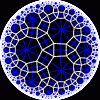
{9,3}
|
| 
| 
| 
| 
| 
| 
| 
| 
| 
{10,3}
|
| 
| 
| 
| 
| 
| 
| 
| 
| 
{20,3}
|
| 
| 
| 
| 
| 
| 
| 
| 
| 
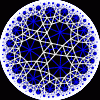
{infinity,3}
|
| 
| 
| 
| 
| 
| 
| 
| 
| 
{infinity,3} | another view
| 
| 
| 
| 
| 
| 
| 
| 
| 
Truncation:
| 0
| .5
| 1
| 1.5
| 2
| 2.5
| 3
| 3.5
| 4 (dual)
| |
Note that the ones based on a regular {p,q} are the same as the ones based on a regular {q,p}, but shown in a different orientation.
The Omnitruncated {3,7} is the "most nearly planar" of all semiregular or regular hyperbolic tesselations, in the sense that if you tried to construct it from Euclidean planar polygons, the sum of the angles at each vertex would be as small as possible while exceeding 360 degrees.
| Omnitruncated | Runcinated | Snub | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| {3,7} |

|

|

|
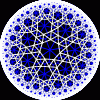
{4,5}
|
| 
| 
| 
| 
{5,5}
|
| 
| 
| 
| 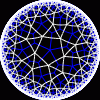
{5,4}
|
| 
| 
| 
| 
{7,3}
|
| 
| 
| 
| 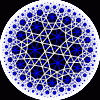
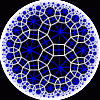
{8,3}
|
| 
| 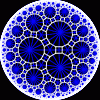
| 
| 
{9,3}
|
| 
| 
| 
| 
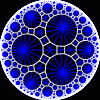
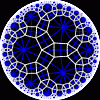
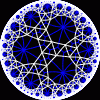
{10,3}
|
| 
| 
| 
| 
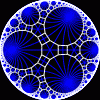
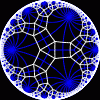
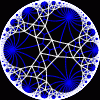
{20,3}
|
| 
| 
| 
| 
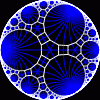
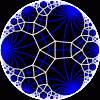
{infinity,3}
|
| 
| 
| 
| 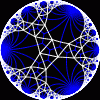
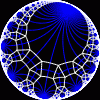
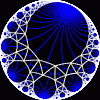
{infinity,3} | another view
| 
| 
| 
| 
|
| Omnitruncated
| Runcinated
| Snub
| |
The dual of the fundamental tiling is composed of "Schwarz polygons" denoted (p0 p1 ... pn-1), with interior angles pi/p0, pi/p1, ..., pi/pn-1, and reflected about their edges.
We can color each vertex of the uniform tiling (or Schwarz polygon of the dual) "even" or "odd" depending on whether it is generated as an even or odd number of reflections of a fixed initial vertex (or Schwarz polygon of the dual, respectively), i.e. whether it is an even or odd distance (number of edges) from the initial vertex.
The resulting tiling is spherical, planar, or hyperbolic, depending on whether the sum of (pi - pi/pi) is <, =, or > 2pi respectively. We can enumerate all possible spherical and planar Schwarz polygons, with corresponding fundamental uniform tilings:
Schwarz Fundamental Vertex Familiar
Polygon Tiling Configuration Name
Spherical:
(2 3 3) (2|3|3|) (4,6,6) truncated octahedron
(2 3 4) (2|3|4|) (4,6,8) truncated cuboctahedron
(2 3 5) (2|3|5|) (4,6,10) truncated icosidodecahedron
(2 2 p) (2<=p<=inf) (2|2|p|) (4,4,2*p) 2p-gonal prism
Planar:
(2 3 6) (2|3|6|) (4,6,12) omnitruncated triangle tiling
(2 4 4) (2|4|4|) (4,8,8) truncated square tiling
(2 2 inf) (2|2|inf|) (4,4,inf) infinity-gonal prism
(3 3 3) (3|3|3|) (6,6,6) hexagonal tiling
(2 2 2 2) (2|2|2|2|) (4,4,4,4) square tiling
Hyperbolic:
All other (p0 p1 ... pn-1), n>=3, pi>=2.
(Note, I haven't proved the above construction works for all cyclic lists
p0,p1,...,pn-1,
but it seems to work for all lists I have tried.
Thus there seems to be a (at least one) uniform
tiling having every conceivable all-even vertex configuration
(2p0,2p1,...,2pn-1).
Note that this construction does
not work in general for vertex configurations
having one or more odd elements;
in fact, for example, there is no semiregular tiling
with vertex configuration (3,4,5) (by this construction
or any other).
Every uniform tiling I know of (with the sole exception of the planar tiling with vertex configuration (3,3,3,4,4)) can be constructed from a fundamental tiling in one of the following ways:
A fundamental tiling (as described above) is denoted by the Coxeter-Dynkin symbol (p0|p1|...|pn-1|). The vertical bar between pi and pi+1 represents the edge type between a 2pi-gon and a 2pi+1-gon in the tiling. When we shrink an edge type to zero size, we remove the corresponding bar in the symbol.
Vertex Familiar
Tiling Configuration Name
(p|q|r|) (2p,2q,2r)
(p|q|r ) (p,2q,r,2q)
(p|q r|) (r,2p,q,2p)
(p q|r|) (q,2r,p,2r)
(p|q r ) (p,q)r
(p q|r ) (q,r)p
(p q r|) (r,p)q
(p||q||r||) (p,3,q,3,r,3)
Spherical:
(2|3|3|) (4,6,6) truncated octahedron
(2|3|3 ) (2,6,3,6) = (6,3,6) truncated tetrahedron
(2|3 3|) (3,4,3,4) cuboctahedron
(2 3|3|) (same as (2|3|3))
(2|3 3 ) (2,3)3 = 33 tetrahedron
(2 3|3 ) (3,3)2 = 34 octahedron
(2 3 3|) (same as (2|3 3))
(2||3||3||) (2,3,3,3,3,3) = 35 icosahedron
(2|3|4|) (4,6,8) truncated cuboctahedron
(2|3|4 ) (2,6,4,6) = (6,4,6) truncated octahedron
(2|3 4|) (4,4,3,4) rhombicuboctahedron
(2 3|4|) (3,8,2,8) = (3,8,8) truncated cube
(2|3 4 ) (2,3)4 = 34 octahedron
(2 3|4 ) (3,4)2 cuboctahedron
(2 3 4|) (4,2)3 = 43 cube
(2||3||4||) (2,3,3,3,4,3) = (3,3,3,4,3) snub cuboctahedron
(2|3|5|) (4,6,10) truncated icosidodecahedron
(2|3|5 ) (2,6,5,6) = (6,5,6) truncated icosahedron
(2|3 5|) (5,4,3,4) rhombicosidodecahedron
(2 3|5|) (3,10,2,10) = (3,10,10) truncated dodecahedron
(2|3 5 ) (2,3)5 = 35 icosahedron
(2 3|5 ) (3,5)2 icosidodecahedron
(2 3 5|) (5,2)3 = 53 dodecahedron
(2||3||5||) (2,3,3,3,5,3) = (3,3,3,5,3) snub icosidodecahedron
(2|2|p|) (4,4,2p) 2p-gonal prism
(2|2|p ) (2,4,p,4) = (4,p,4) p-gonal prism
(2|2 p|) (same as (2|2|p))
(2 2|p|) (2,2p,2,2p) = (2p,2p) 2p-gonal dihedron
(2|2 p ) (2,2)p 2p lunes of ambiguous width
(2 2|p ) (2,p)2 = p2 p-gonal dihedron
(2 2 p|) (same as (2 2|p))
(2||2||p||) (2,3,2,3,p,3) = (3,3,p,3) p-gonal antiprism
Planar:
(2|3|6|) (4,6,12) omnitruncated hexagon or triangle tiling
(2|3|6 ) (2,6,6,6) = 63 regular hexagon tiling
(2|3 6|) (6,4,3,4) runcinated hexagon or triangle tiling
(2 3|6|) (3,12,2,12) = (3,12,12) truncated hexagon tiling
(2|3 6 ) (2,3)6 = 36 regular triangle tiling
(2 3|6 ) (3,6)2 bitruncated hexagon or triangle tiling
(2 3 6|) (6,2)3 = 63 regular hexagon tiling
(2||3||6||) (2,3,3,3,6,3) = (3,3,3,6,3) snub hexagon tiling
(2|4|4|) (4,8,8) truncated square tiling
(2|4|4 ) (2,8,4,8) = (8,4,8) truncated square tiling
(2|4 4|) (4,4,4,4) = 44 square tiling
(2 4|4|) (same as (2|4|4))
(2|4 4 ) (2,4)4 = 44 square tiling
(2 4|4 ) (4,4)2 = 44 square tiling
(2 4 4|) (same as (2|4 4))
(2||4||4||) (2,3,4,3,4,3) = (3,4,3,4,3) snub square tiling
(2|2|inf|) (4,4,inf) infinity-gonal prism
(2|2|inf ) (2,4,inf,4) = (4,inf,4) infinity-gonal prism
(2|2 inf|) (same as (2|2|inf))
(2 2|inf|) (2,inf,2,inf) = (inf,inf) infinity-gonal dihedron
(2|2 inf ) (2,2)inf (not really meaningful)
(2 2|inf ) (2,inf)2 = inf2 infinity-gonal dihedron
(2 2 inf|) (same as (2 2|inf))
(2||2||inf||) (2,3,2,3,inf,3) = (3,3,inf,3) infinity-gonal antiprism
(3|3|3|) (6,6,6) = 63 regular hexagon tiling
(3|3|3 ) (3,6,3,6) bitruncated hexagon or triangle tiling
(3|3 3 ) (3,3)3 = 36 regular triangle tiling
(3||3||3||) (3,3,3,3,3,3) = 36 regular triangle tiling
(2|2|2|2|) (4,4,4,4) = 44 square tiling
(2|2|2|2 ) (2,4,4,2,4,4) = 44 square tiling
(2|2|2 2 ) (2 4 2 4)2 = 44 square tiling
(2||2||2||2||) (2,4,2,4,2,4,2,4) = 44 square tiling
Hyperbolic:
For (p-2)*(q-2) > 4:
(2|p|q|) (4,2p,2q) omnitruncated {p,q} or {q,p}
(2|p|q ) (2,2p,q,2p) = (2p,q,2p) truncated {p,q}
(2|p q|) (q,4,p,4) runcinated {p,q} or {q,p}
(2 p|q|) (p,2q,2,2q) = (p,2q,2q) truncated {q,p}
(2|p q ) (2,p)q = pq {p,q}
(2 p|q ) (p,q)2 bitruncated {p,q} or {q,p}
(2 p q|) (q,2)p = qp {q,p}
(2||p||q||) (2,3,p,3,q,3) = (3,p,3,q,3) snub {p,q} or {q,p}
(3|4|5|) (6,8,10)
(3|4|5 ) (3,8,5,8)
(3|4 5|) (5,6,4,6)
(3 4|5|) (4,10,3,10)
(3|4 5 ) (3,4)5
(3 4|5 ) (4,5)3
(3 4 5|) (5,3)4
(3||4||5||) (3,3,4,3,5,3)
(3|2|2|2|) (6,4,4,4) NOT the same as runcinated {6,4}, see below
(3|2|2|2 ) (3,4,4,2,4,4) = (3,4,4,4,4)
(3|2|2 2|) (2,6,4,2,4,6) = (6,4,4,6)
(3|2|2 2 ) (3,4,2,4)2 = (3,4,4)2
(3 2|2|2 ) (2,4,2,4)3 = 46
(3|2 2 2|) (2,6,2,6)2 = 64
(3||2||2||2||) (3,4,2,4,2,4,2,4) = (3,4,4,4,4)
XXX TBD