Triangle stripifier

Converting sets of triangles with shared edges into triangle strips

(Source code is now available.)

A 3-d computer graphics application using an accelerated polygon rasterization system must pass vertices for each polygon it displays on the screen. Many object models are created using spline patches of some sort and then polygonized before rendering. I will limit my discussion to triangles, into which all polygons may be split. Typically, most of the triangles generated share edges and thus vertices. It is inefficient to pass all three vertices to the rendering toolkit, as it then performs multiple viewing and screen transformations for the same vertex several times.

Triangle strips allow 3-D applications to perform fewer per-vertex operations by passing a set of triangles, each of which in turn shares an edge with the previous triangle. In this way, instead of transforming

	3 * n

vertices, the renderer transforms

	2 + n

vertices and renders the same number of triangles.

Initial data set

I used one patch of the Utah teapot bezier definition to make the following set of connected triangles.

I used the same data set with 30% of the triangles removed randomly.

I also used the data with 50% of pairs of triangles with their vertices rotated.

(These images were rendered with the toolkit I used to make my computer graphics page.)

Input restrictions

The triangles were passed in a random order to a stripifier program, in the following data format:

	#vertices
	vertexX vertexY vertexZ normalX normalY normalZ
	...
	#triangles
	vertex_1_index vertex_2_index vertex_3_index
	...

It's apparent that this data is less difficult to process than, say, a list of triangles specifiying the actual vertex coordinates, in which a separate processing step must be included to determine which vertices are shared. However, I don't think that the data format I have mentioned is unreasonable to expect from most applications. An even better format would be a list of edges and then a triplet of edge indices for each triangle.

A first-cut algorithm

A possible algorithm to convert the above data into strips would be to pick a random triangle and simply make a strip arbitrarily. Although this is better than passing just triangles, there are many small strips and single triangles which are isolated by this scattered approach.

(The algorithm presented here was generated for a rendering pipeline of which optimal strip length is 14 vertices.)

Here's the result of a "greedy" algorithm to convert the above data set to strips, using 26 strips, averaging 6.2 triangles per strip:

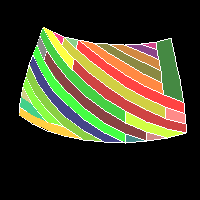
Here's the greedy output for the second set of data, using 35 strips, averaging 3.1 triangles per strip:

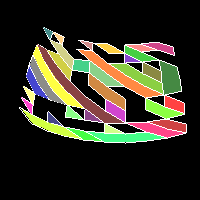
Here's the greedy output for the third set of data, using 37 strips, averaging 4.4 triangles per strip:

Considering the problem further

The goal of this exercise is to reduce the number of vertices passed, to minimize the number of vertices processed and therefore matrix multiplications, perspective divides, etc. The number of vertices passed is

	numStrips * 2 + numTriangles

because each strip requires two vertices for initialization, and then each triangle requires one more vertex. Because of this relationship, the goal of the algorithm may be to reduce the number of strips, leading to the same result. Two suboptimal strips made from a series of triangles would be better than one optimal strip and two even worse strips. A possible smarter algorithm might perform a kind of seed fill, starting from triangles that are only 1-connected. This would favor fewer strips by reducing the number of breaks in the data set.

Considering the input data

The data sets used here are not representative of normal data. It is my opinion that most polygon data is provided in a format which is already close to optimal. That is, successive triangles will tend to share edges. I expect most applications would be producing output from bicubic patches of some kind, or otherwise regularly tesselated surfaces. The algorithms used here could be improved by a switch indicating the original form of data, i.e. a degree to which the original data was strippable without manipulation.

Sample implementation

Source code is now available.

This code makes the assumption that only one or two triangles share an edge. This could easily be false, say in the case of the tail of a dart.

The sample implementation has been compiled and tested on a PowerBook 180 with MachTen 2.1.1 and a 486 workstation with Linux 1.2.13.

512 by 512 JPEGs of the results

Brad Grantham