Physically-Based Fluid Modeling using Smoothed Particle Hydrodynamics

Table of Contents
Chapter 4: Results



CHAPTER 3

Implementation

The fluid modeling method presented here is based on a spatially coupled particle system. Particles represent small fluid elements which interact according to the laws of hydrodynamics. The particles are Newtonian, that is, they are governed by Newton's laws of motion and their accelerations are determined by gravitational and pressure forces. Particle system dynamics are based on Smoothed Particle Hydrodynamics, but use a different equation of state and do not require artificial viscosity, the XSPH variant or the thermal energy. Particles can be rendered individually or represented by an implicit surface. A user interface is used to turn on and off these features and for modifying the input parameters. This chapter describes the implementation details of the dynamics and rendering as well as collision handling. Also covered are the details of the software architecture, including data structures.

3.1. Particle Attributes

Each particle has the following attributes: In addition the particle system has a uniform smoothing length (h) and ratio of specific heats ().

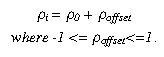
Particles are given an initial position, velocity and thermal energy. An initial density is specified (usually 1000 kg/cm³ ), but is then adjusted by a small amount for individual particles:

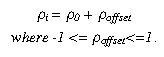
Without this minor adjustment all of the initial particle densities are equal which causes the equation of state to calculate a uniform initial pressure of 0. Without a pressure gradient there is no acceleration, and also no change in density, so the system goes nowhere. The initial mass is then set according to:

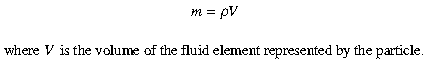
After a particle has been initialized, its initial pressure is calculated using the equation of state, and the particle is added to a list maintained with a cell-type data structure designed to efficiently manage force calculations.

3.2. Data Structures

Spatially coupled particle systems require N² computations in order to compute forces for all particles. In order to minimize this computation and take advantage of the limited particle interaction offered by the kernel, the data volume is divided into cells. A cell can have many particles, but each particle is associated with only one cell and interacts only with particles in neighboring cells. The particle distribution is determined once at the beginning of each time step with a single pass through the particle list. Calculations requiring inter-particle computations are then performed by traversing the cells. Figure 2 shows a conceptual diagram of the cell volume configuration.

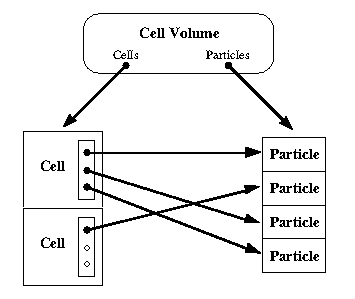
A CellVolume data structure contains the main list of particles and a 3D array of particle Cell structures, each containing a linked list of pointers to particles in the main list. The size of each cell is approximately double the smoothing length (it is approximate since 2*h may not be an even divisor of the volume extent). The cell volume is reallocated only when the smoothing length is changed. The particles are redistributed at the beginning of each time step since particles may have moved to a new cell during the last time step. Each cell also contains a flag, set only if there are particles in the cell, for use during rendering (see section 3.5).

Figure 2. Cell Volume data structure.

3.3. Dynamics

The equations used to calculate forces among particles are nearly identical to the incompressible SPH equations described in section 2.2. A notable exception is the equation of state, which is discussed below. Some of the SPH equations were designed to handle specific situations in a fluid simulation (e.g. artificial viscosity is added to handle shock waves). Since most of these situations are not expected to occur in these animations the equations were made optional, controlled by toggle buttons in the user interface. The following is an outline of the computations during one time step, including the associated equation numbers referring to equations in section 2.2. The subsequent descriptions detail the areas which differ from the standard SPH equations. 
1. Update rates of change: 
    for all particles 
        calculate acceleration due to pressure gradient (equation 2.7) 
        calculate rate of change of thermal energy (equation 2.8) 
        calculate rate of change of density (equation 2.6) 

2. Handle collisions 

3. Update positions: 
    for all particles 
        calculate XSPH velocity variant (equation 2.10)

    for all particles 
        update position, velocity (using leap-frog integrator) 
        update thermal energy 
        update density 

4. Update pressures: 
    for all particles 
        compute pressure using modified equation of state 
        compute speed of sound 

5. Adjust time step
1. Update rates of change: The standard SPH equations are used for the momentum and thermal energy equations. The smoothed version of the continuity equation is used as well. The artificial viscosity equation from standard SPH is included, but is optional. The kernel used in these equations is the same as equation 2.5. Since the thermal energy is not used in this equation of state (where it normally is used in compressible flows) the computation of its rate of change is irrelevant and is usually turned off.

2. Handle collisions: Collision detection and response is discussed in section 3.4.

3. Update positions: The XSPH velocity variant is included, but is optional. The leap-frog method of integration is used for particle integration. Velocities are updated at intervals midway between time steps, giving a higher accuracy than the standard Euler method. If vi and xi represent velocity and position at time i then:

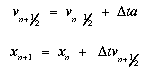
The velocity used in the SPH equations is then calculated according to:

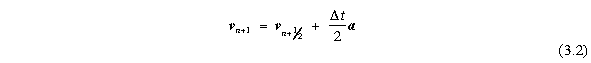
The XSPH variant is added to the velocity used in updating the position, but is not included in the SPH velocity.

4. Update pressures: Upon careful inspection using dimensional analysis it was found that the constant B in Monaghan's equation of state (equation 2.11) was incorrect (Bryan, 1995, personal communication). The corrected version is:

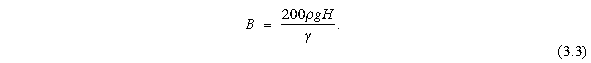
With  in the numerator the units now match those of pressure (Pa, or kg/ms² ) and the equation of state now returns the proper pressure values. The speed of sound c for each particle is computed using:

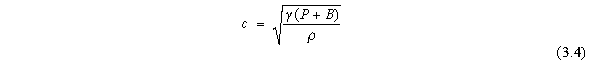
5. Adjust time step: The algorithm for adjusting the time step is based on the Courant condition:

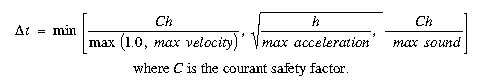
This algorithm was designed to prevent information from traveling too far during one time step. Information can travel at three possible speeds: the velocity of the flow (i.e. the particle velocity), the velocity of sound, or at a velocity determined by the acceleration of the flow (i.e. looking into the future beyond where the current velocity will take the particle). Each speed restricts the length of the time step; the algorithm chooses the smallest.

3.4. Obstacles

Obstacles are implemented as a list of large polygons. Each polygon is one "face" of an obstacle. For example a funnel is created out of six polygons, making a hexagonal shape, and a floor is one square covering the bottom face of the data volume. Figure 6, Appendix, shows two of the obstacles used in this research. After integration, each particle is checked against all faces of all obstacles. Collisions are detected using the particle/plane method described in section 2.1.3. Several methods of responding to collisions were implemented and tested. The two which met with the most success were bouncing the particle and repelling the particle. Bouncing a particle involves modeling an inelastic collision through the use of contact forces and velocity modification. Essentially the normal components of the particle's acceleration and velocity are canceled, leaving components which are tangential to the obstacle face (See Figure 3.) As a result the particle comes to rest on a flat surface, or slides down a sloped surface.
Figure 3. Inelastic collision.

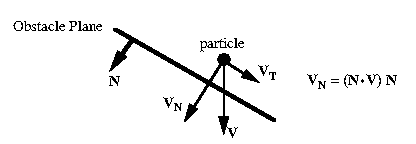
Repelling a particle is a more gradual process. Each obstacle face applies a repulsive force to nearby particles, similar to the repulsive forces described in section 2.1.3. The force is inversely proportional to the distance between a particle and the obstacle. See Figure 4.

Figure 4. Repulsive collision.

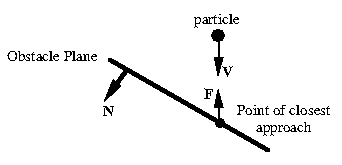
Repelling a particle works well for situations where particles are initially near an obstacle (i.e. a breaking dam or a static container of water). If a particle has a significant velocity when approaching the obstacle (i.e. falling water) the velocity can carry it too near the obstacle resulting in a very strong repulsive force which can throw the particle away from the obstacle with an abnormally high velocity. Although the time step will get adjusted according to the large acceleration and velocity, it does not properly handle the large abrupt change which happens in this case.

On the other hand, particle bouncing works well for falling particles, but prevents any "splashing" motion since all acceleration and velocity normal to the obstacle plane is canceled. The resulting motion has a viscous feel to it, which is fine when modeling oil or slime, but not water.

3.5. Rendering

In this system particles can be rendered individually as spheres or as a surface. The surface is computed using the blobby method described earlier in section 2.1.4, and is then polygonized using a variant of the marching cubes algorithm (Lorensen and Cline, 1987). Although the surface representation results in a more realistic looking model, the additional computation required is a significant performance bottleneck. This section describes the surface generation algorithm and the attempts that were made to improve the speed.

Generating an implicit surface can be broken down into two major steps: generating the implicit field (hereafter referred to as evaluation since the implicit function is being evaluated to generate the field), and generating the actual polygons to be displayed (hereafter referred to as polygonization).

For these calculations the data volume is divided into voxels (not to be confused with the cells described earlier; there are many voxels within a given cell). Traditionally the evaluation step is carried out by evaluating the implicit function at every voxel, summing over all particles:

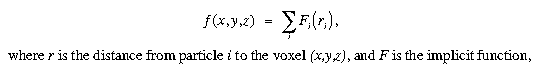
resulting in a 3D volume of scalar values. That volume is then sent in its entirety to the polygonizer, which outputs a list of polygons with normals for the graphics engine to render.

Evaluating the implicit function at every voxel for every particle is the bottleneck for surface generation. Several different approaches were taken in an attempt to improve the efficiency of the algorithm by taking advantage of the cell partitioning in which the particles reside.

Initially it was thought that surface generation could be restricted to those cells which contain particles, ignoring all empty cells. Unfortunately the surface is not always contained within the occupied cells. A surface is offset from the particles enough that it often ventures into neighbor cells. The resulting surfaces had chunks taken out of them where empty cells had been ignored.

The next attempt involved loosening the restriction to include the empty neighbor cells. In other words, now cells which either contained particles or were next to cells with particles were considered for surface generation. Each cell was evaluated and polygonized independently (assuming eventual parallelization). The problem with this method is that the polygonization algorithm requires data from adjoining cubes for a complete surface. Otherwise there are gaps in the surface along cell boundaries.

Instead of trying to duplicate data (hence duplicating calculations) it was decided that the surface evaluation and generation would be decoupled. The data volume is zero-filled and the voxels in marked cells are evaluated as before. The polygonizer then processes the data volume in its entirety, which is essentially the traditional method of implicit surface generation with the exception of the marked cells.

The polygonizer is a parallel implementation of the marching cubes algorithm (Lorensen and Cline, 1987). Marching cubes is a surface construction algorithm which analyzes each voxel of a scalar data volume in order, first determining if there is a surface intersecting the voxel and then computing the polygons of the surface within the voxel. Edge coherence is used to take advantage of the fact that voxels share edges and therefore share triangle vertices. Each voxel inherits many of its triangle vertices from the previous pixel, row or slice of data. The implementation used here also analyzes each voxel of the volume but does so in parallel, so there are no "previous" pixels, rows or slices to inherit from since cubes can be processed in any order. The solution to this problem is the use of a hash tree for storing vertices and normals as they are calculated for each processor. The caveat for this solution is the merging required after all voxels are processed: if there are a large number of polygons stored in each processors hash tree it takes a significant amount of time to combine all of the trees into one polygon list needed for rendering. As a result it is inefficient to run this algorithm on surfaces with large numbers of polygons (greater than ~50K for a 96³ volume, ~20K for a 32³ volume). The surfaces generated when modeling fluid are generally much smaller than this, therefore this bottleneck was not an issue.

3.6. Parallelization Methods

The particle nature of this modeling method lends itself well to parallelization. Both the surface generation and part of the SPH calculations were designed to run in parallel. The code is written in C using IRIS Power C, the multiprocessing C compiler from Silicon Graphics Inc. (SGI). The code is parallelized by the insertion of compiler directives, which can be ignored by any non Power C compiler, enabling the code to run in serial on any platform.

The slowest portion of the SPH calculations was updating the rates of change because it requires computations over all pairs of particles. This is the only loop which was parallelized. (The XSPH calculation also requires N² computations but was not parallelized, causing a significant slow down with large numbers of particles when this option is enabled. However, the XSPH variant generally has very little contribution to these SPH simulations (see Chapter 4) and so is rarely used.)

The rates of change update loop processes each cell to calculate interactions among its particles and its neighbor cells' particles. Since each particle is in one and only one cell, the cells can be processed independently, in parallel. Inserting pragmas around the loop tells the Power C compiler that this loop can run in parallel. When compiled on a multi-processor SGI system the compiler creates a function out of the loop which is then forked (using the m_fork system call) once for each available processor. Cells are distributed among the processors by the multitasking scheduler. Load balancing (how many cells get assigned to each processor in what size chunks) can be controlled using pragmas or by setting system environment variables. For more information on Power C and SGI multi-process programming see (Bauer, 1992; Graves, 1993).

The surface is evaluated in a similar manner: cells are distributed among available processors and are evaluated independently. The polygonization algorithm is more of a fine-grained parallelization, distributing voxels across processors instead of cells.

3.7. Software Architecture

In order to preserve interactivity the SPH calculations are run in a separate process from the user interface and rendering computations. The two processes communicate via shared memory, where all of the major data structures are stored. Figure 5 shows a diagram of the software architecture, including indications of data flow.
Figure 5. Shared memory configuration.

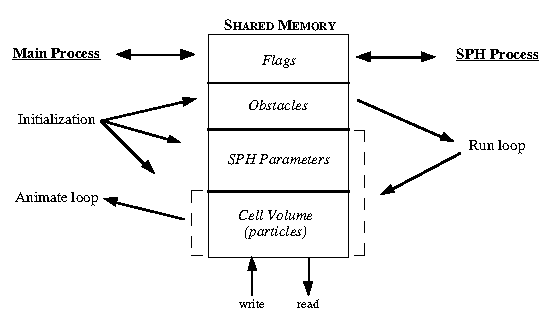
The data structures are described as follows:

Flags: Messages between processes such as "start run" and "reset system".
Obstacles: List of polygons which the particles are not allowed to cross through.
SPH Parameters: Variables in SPH equations (e.g. the smoothing length h).
Cell Volume: Particle system and cell structures.
The main process only writes into shared memory when initializing the system with a new particle set or obstacles. After that the SPH process is updating the Cell Volume block and the SPH block during each time step. The main process has its own local copy of the Cell Volume which it uses for drawing and surface rendering. There is no handshaking between the two processes: the SPH process runs as fast as it can, and the main process updates its local copy as fast as it can by copying from shared memory after each surface is rendered. This decouples the visual update from the numerical update, allowing multiple time steps to be run between each frame. Since the time steps are fairly small (on the order of 0.001 to 0.0001 seconds), usually there is little visual information being lost by not rendering a surface for every time step. Figure 7, Appendix, is a graph showing update rates for a 156 particle simulation. The tall spikes (dashed lines) are time steps where the surface generator completed its update. The graph shows not only the relative update rate (approximately 1 surface for every 5-6 time steps in this situation), but also the relative computation time (a surface computation takes much longer than an SPH time step computation, about 3 times longer in this particular simulation). It is possible to turn off surface rendering and see the individual particle rendering which can update as fast as the SPH computations run.

Top
Chapter 4: Results